The module should contain a class `SimpleOption` that will satisfy the following documentation. The option class here is super trivial, but it demonstrates an architectural approach: encapsulate assets via their contract terms, and pass that to pricing and risk functions.  A slightly more advanced approach would have a similar data container for the "market environment" (prices, risk free rate, volatilities...) that would also be passed to those functions.

```

class SimpleOption

Simple option contract class capturing the key features of a put or call option. This is just a simple data container.

Parameters

----------

strike : float

    strike price for option

is_call : boolean, default True

    flag for indicating if the option is a put or a call.

    True for call, False for put

Attributes

----------

strike : float

    strike price for option

is_call : boolean

    flag for indicating if the option is a put or a call.

    True for call, False for put

```

The module should also contain the three following methods, and should satisfy the following documentation:

```

bs_price(option, spot, ttm, vol, rate)

    Black-Scholes option price for the given market values.

    Parameters

    ----------

    option : SimpleOption

        The option to price

    spot: float

        Current spot price of underlying stock

    ttm : float

        remaining time to maturity in years

    vol : float

        annualized volatility of the option's underlying stock

        15% would be passed as 5.0 and not 0.15

    rate : float

        annualized riskfree interest rate, as a percent

        5% would be passed as 5.0 and not 0.05

    Returns

    -------

    price : float

        The Black-Schole price for this option

bs_implied_vol(option, spot, ttm, price, rate)

    Black-Scholes implied volatility for the given market values.

    Parameters

    ----------

    option : SimpleOption

        The option to price

    spot: float

        Current spot price of underlying stock

    ttm : float

        remaining time to maturity in years

    price : float

        current price of option

    rate : float

        annualized riskfree interest rate, as a percent

        5% would be passed as 5.0 and not 0.05

    Returns

    -------

    vol : float

        The Black-Schole implied volatility for this option

bs_greeks(option, spot, ttm, vol, rate)

    Black-Scholes "greeks" for the given values.

    Parameters

    ----------

    option : SimpleOption

        The option underlying the calculations

    spot: float

        Current spot price of underlying stock

    ttm : float

        remaining time to maturity in years

    vol : float

        annualized volatility of the option's underlying stock

        15% would be passed as 5.0 and not 0.15

    rate : float

        annualized riskfree interest rate, as a percent

        5% would be passed as 5.0 and not 0.05

    Returns

    -------

    (delta, vega, theta, gamma) : tuple(float)

        The Black-Scholes sensitivities to various parameters.

        delta : sensitivity to change in stock price

        vega : sensitivity to change in volatility

        theta : instantaneous "time-decay" sensitivity

        gamma : sensitivity of the option delta to change in stock price

```

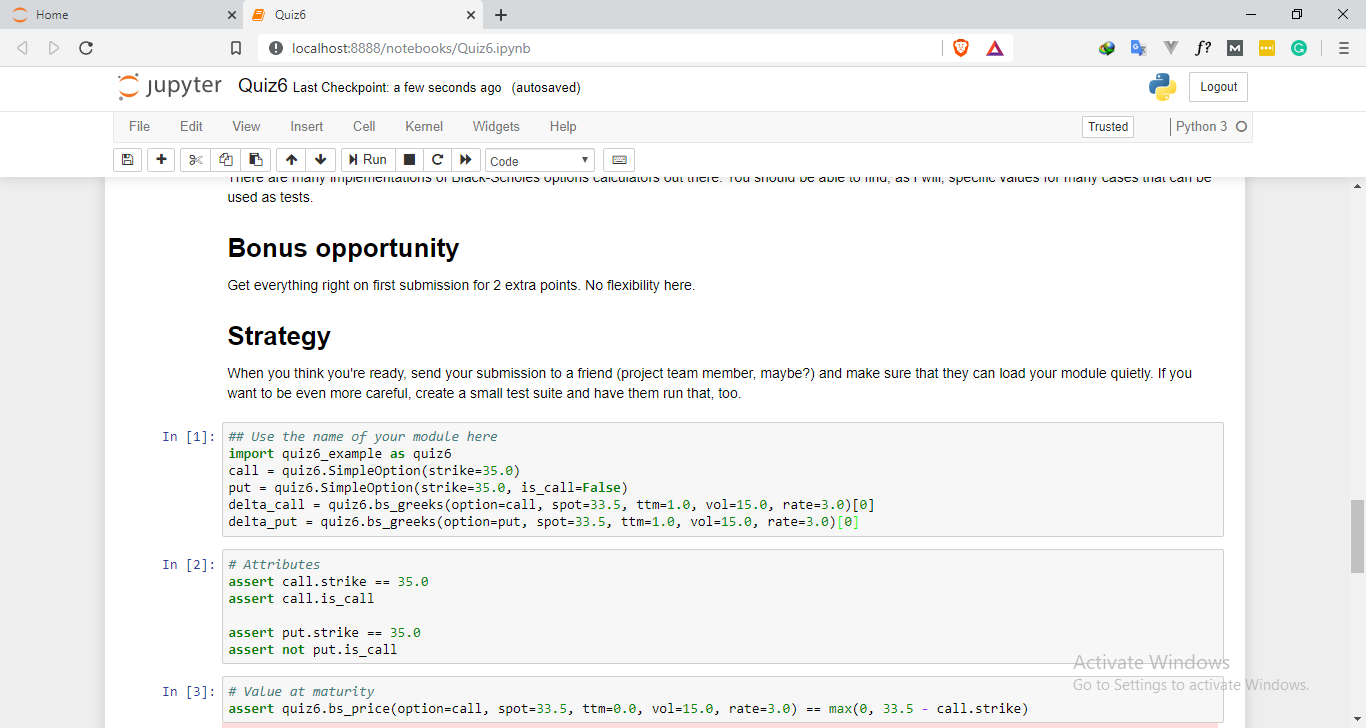
## Basic tests

* A call with zero time-to-maturity has value max(0, price-strike), and a put with zero ttm has value max(0, strike-price). 

* Put-call parity implies that $\Delta(call) - \Delta(put) = 1$ for a put and a call written against the same stock having the same strike and maturity (under the same market assumptions about volatitility and the risk-free rate, naturally).

This assignment has been answered 2 times in private sessions.

Or buy a ready solution below.